Sampling
Sampling data can be done in many ways depending on what is desired. Most often a random uniform sampling is used to collect a small subset for preliminary analysis. This can reduce computation and provide rapid insight. There are, however, other reasons to sample data, such as create a representative sample set that covers the data range.
A particular example arises in earth sciences when the goal is to model weather or ocean conditions across the range of possible forcing. In the case of waves, model forcings would need to cover the range of wind speeds, directions, water levels, and current conditions expected. Typically buoys or wind stations would be used to provide a time series of these forcing variables and from those, determine a manageable subset of conditions to model waves for (numerical wave models can be computationally costly!). For further reading see Camus et al
Random uniform sampling would be a poor choice in this example. It is very likely that benign calm conditions are common while storm conditions are rare, and therefore a random sample would tend to select many similar conditions, while ignoring rare but important events.
Sampling with maximum dissimilarity
To improve coverage across plausible conditions we could instead use the maximum dissimilarity sampling algorithm, that maximizes the distance (L2-norm by default, but is user determined) between samples in data-space. To illustrate how different this approach is I’ll share two examples, the first a subsampling of uniformly random data with two dimensions (for simplicity, this approach can be extended to N dimensions). Below we sample from the data (grey) using a random uniform sampling (left) and maximum dissimilarity sampling (right).
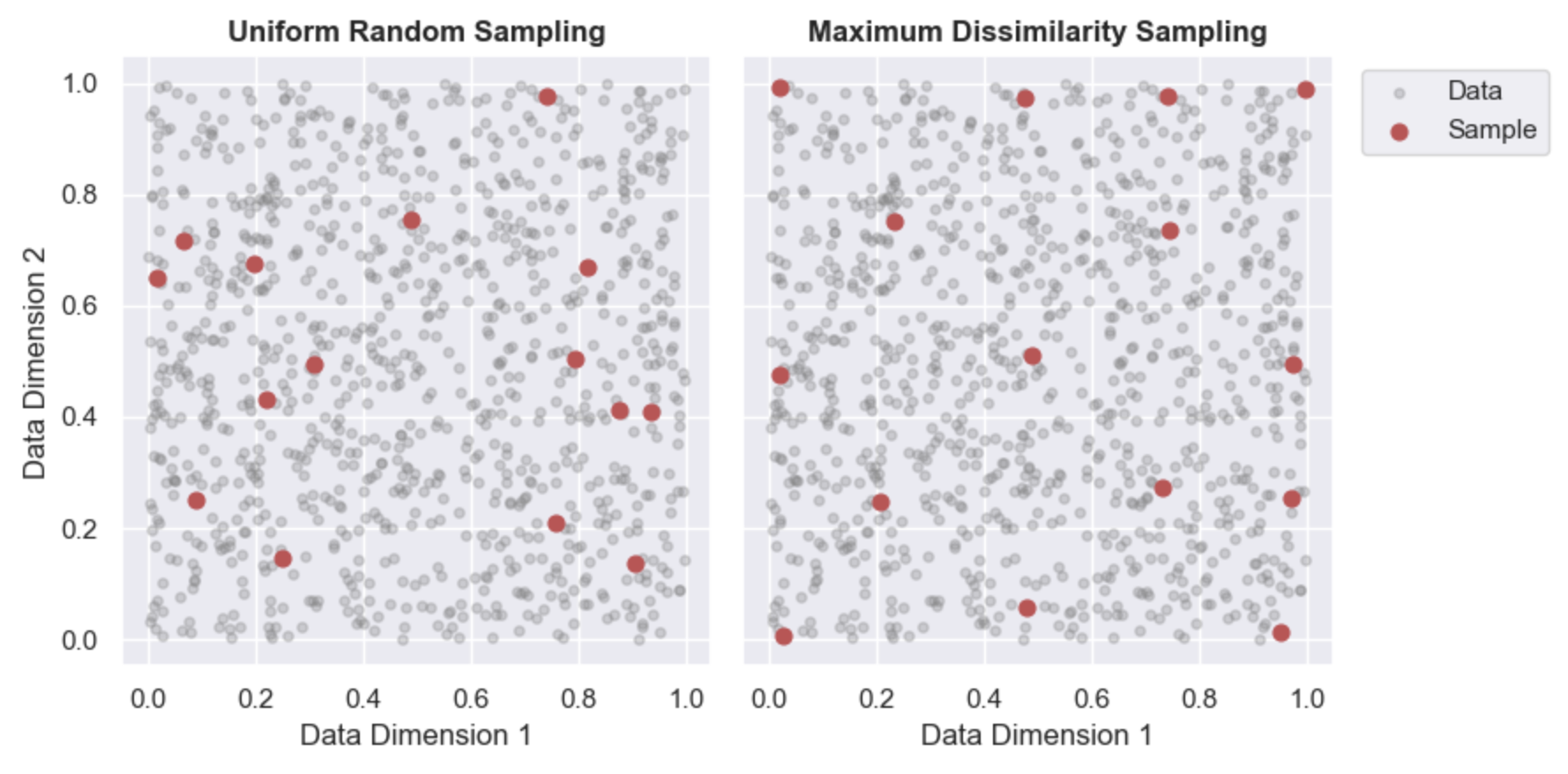
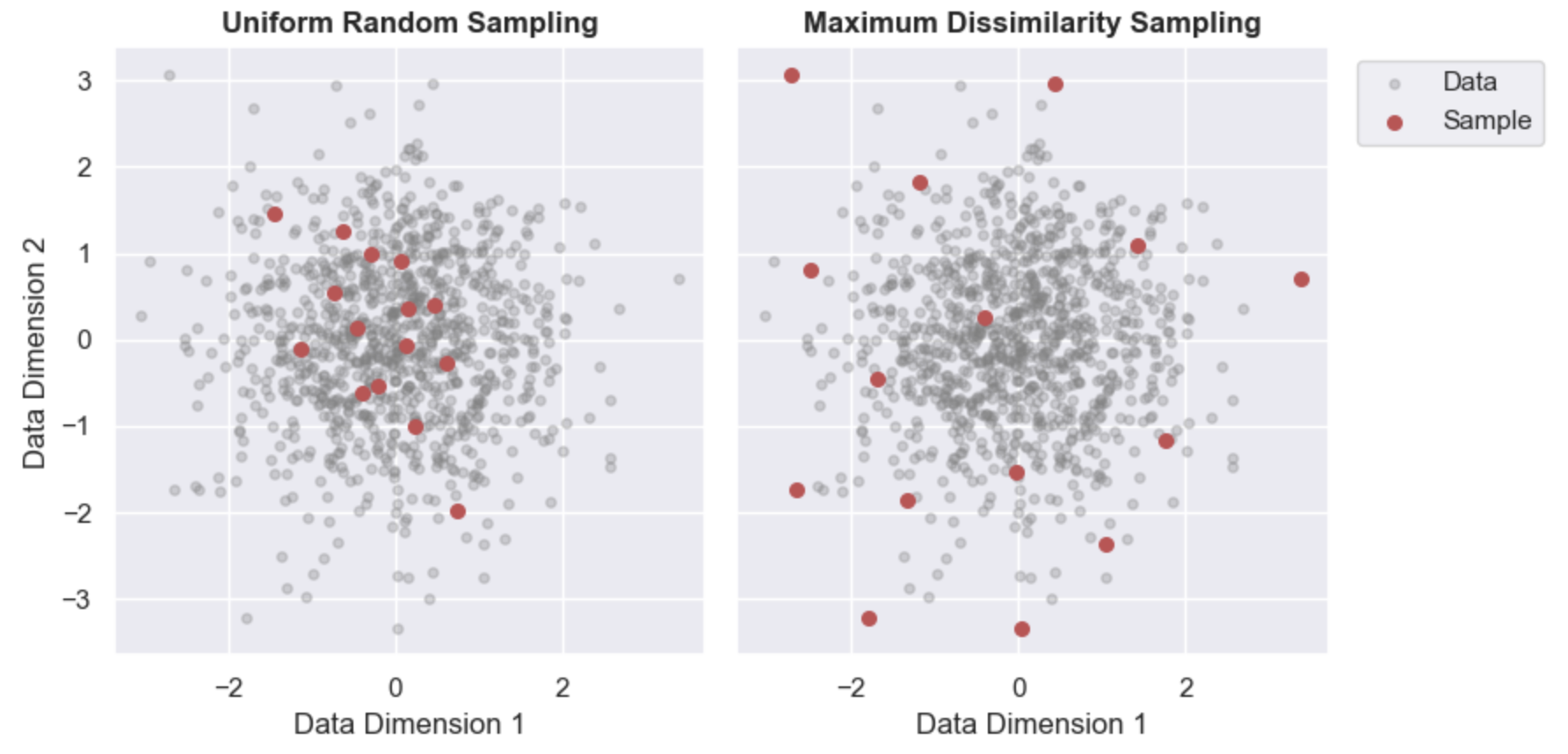
While similar, we can quickly see that using maximum dissimilarity results in samples along the edge of the data-range. Additionally, the samples are more evenly spaced (L2-norm applied here). The difference between these approaches becomes even more clear with non-uniformly spaced data. Shown below is the same comparison but with Guassian distributed random data. Here, the contrast is more stark because random sampling will provide more samples where the data is denser. In this case the subset created with maximum dissimilarity is significantly better at capturing the range in data values.
Please see mda.py in my repository, handy_data_tools for the algorithm implementation and an example. Feel free to contact me with any questions or thoughts!